統計的な有意差とは、得られたデータが単なる偶然ではなく、意味のある違いを示していることを確認するためのものです。統計的な有意差を確認するためには有意差検定という手法が用いられます。この手法では、データの背後にある仮説を検証し、サンプル間の違いが偶然によるものなのか、それとも実際に存在するのかを定量的に評価します。
標準的な有意差検定の手順には、まず帰無仮説と対立仮説を設定し、次に適切な検定法(t検定、カイ二乗検定、ANOVAなど)を選びます。その際、p値が統計的有意水準(通常0.05)未満である場合、帰無仮説を棄却し、データ間に有意差があると結論づけます。※p値や帰無仮説についての説明はこちら。
統計を学ぶ学生や研究者にとって有意差検定の基本概念は必須です。注意すべき点として、サンプルサイズの影響や多重検定問題があります。これらの要因を十分に考慮することで、より信頼性の高い結論を導くことができます。
有意差とは?
統計的な有意差とは、観測された差が単なる偶然ではなく、統計的に意味のある差であることを示します。統計的有意差がある場合、その差は統計的手法を用いて検証され、確証された結果と見なされます。検定手法にはt検定やカイ二乗検定などがあり、これらを正しく利用することでデータに基づく結論を信頼性高く導くことができます。重要なのは、検定実施時の注意点として適切なサンプルサイズと正確な実験デザインを確保することです。それにより、誤差やバイアスを最小限に抑え、実際の有意差を正確に判断することが可能です。
※t検定についてはこちら。
有意差の基本概念
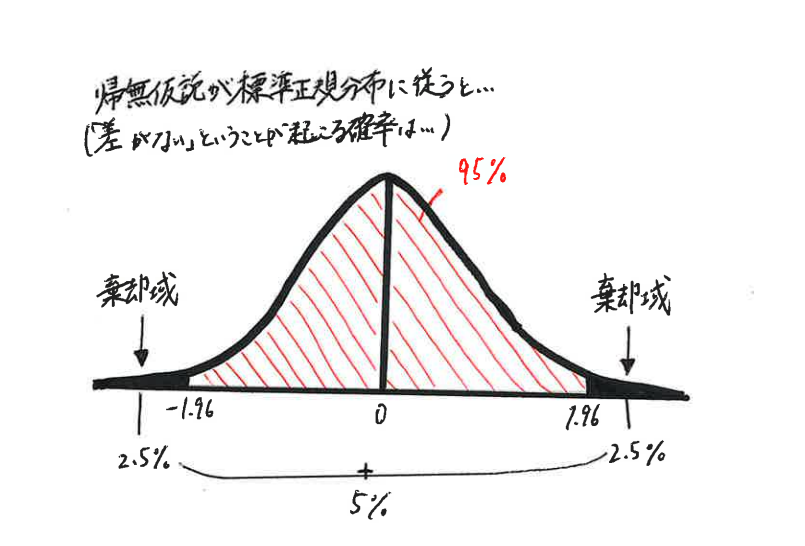
有意差は、データ間の差が統計的に有意かどうかを検証し、偶然ではなく実際の差異に基づくことを確認する概念です。統計的有意差を判断する主な手法としてp値が使用されます。通常、p値が5%(0.05)以下であれば、その差は有意と見なされます。p値とは、統計学における仮説検定において、帰無仮説(※「差がない」という仮説。H₀)が成立する確率のことを示しており、「差がない」という仮説が標準正規分布に従うとして考え、得られた検定統計量の実現値(Z)が有意水準5%の棄却域に入ると(Z≦-1.96または1.96≦Z)、「差がないという確率は5%以下でしか起きない」ということになり、つまりは「95%以上の確率で差がある」ということであり、「有意な差がある」と判断されるということになります。そのため、p値が小さいほど観察された差が偶然である確率が低いことを意味します。このため、p値が低い場合、データ間の差が統計的に有意であると認識されやすくなります。統計的有意差を理解し、適切な検定手法を用いることは、正確なデータ分析に不可欠です。

統計における有意差の重要性
データ分析や研究において、有意差を確認することは非常に重要です。これにより、データに基づく結論や提言の信頼性が高まり、確証バイアス(自分にとって都合のいい情報ばかりを無意識的に集めてしまい、反証する情報を無視したり集めようとしなかったりする傾向のこと)を避けることができます。具体的には、臨床試験で薬の効果を確認し、マーケティング戦略の効果を測定する場合など、多くの分野で有意差の検定が重要な役割を果たします。有意差を理解し、正確に検定することで、科学的な意思決定がより信頼できるものとなります。統計的有意差が意味する基本概念や適切な検定手法、実施時の注意点を熟知することは、統計を学ぶ学生や若手研究者、データ分析に関心のあるビジネスパーソンにとって重要です。
有意差検定とは?
統計学における有意差検定とは、名前の通り、有意差の有無を検定するもので、データに基づき二つ以上のグループ間で差が偶然でないかを統計的に判断する手法のことを指します。これにより、グループ間の差を具体的かつ客観的に評価できます。有意差検定は、事象の因果関係や効果の測定など、多くの場面で有用です。基本的な流れとしては、まず仮説を設定し、その後統計量を計算し、最終的に有意水準を基に結果を解釈します。特に、統計的有意差を見逃さないためには、適切な検定手法の選択やデータの前処理が重要です。
有意差検定の基本的な流れ
有意差検定のプロセスは以下の数ステップに分けられます。まず、仮説を設定します。これは一般的に帰無仮説と対立仮説の二種類です。次に、サンプルを収集し、データの前処理を行います。続いて、適切な検定手法を選びます。t検定やカイ二乗検定などから検定手法を選択して統計的有意差を検証します。最後に、結果を解釈し、帰無仮説を棄却するかどうかを判断します。これらのステップを順守することで、統計的有意差の検証を正確かつ信頼性の高い形で実施できます。
仮説検定と有意差検定
仮説検定と有意差検定は、統計的データ分析に欠かせない手法です。仮説検定とは、母集団に関する仮説を設定し、その仮説がデータに基づきどれだけ支持されるかを検証する方法です。一方、有意差検定はデータ間の差異が偶然によるものではなく、統計的に有意であるかどうかを判断します。これらの検定は研究結果の信頼性を評価するために不可欠です。例えば、t検定やカイ二乗検定などの手法があります。仮説検定と有意差検定の理解は、データ解析において正確な結論を導くために重要です。
仮説検定の基本概念
仮説検定は、ある仮説が正しいかを統計的手法で検証するプロセスです。具体的には、以下の手順を踏みます:
まず、帰無仮説(H0)を設定します。これは検定対象となる母集団の特性についての仮説です。例えば、「新薬Aの効果は既存薬と同じである」とします。次に、対立仮説(H1)を設定します。これは、帰無仮説が正しくない場合に成立する仮説で、「新薬Aの効果は既存薬よりも優れている」などです。
続いて、検定統計量を計算します。サンプルデータを基に検定統計量を計算し、データの変動を示します。次に、検定統計量を用いてp値を計算します。p値は帰無仮説が正しい場合に観察されるデータの確率です。最後に、事前に設定した有意水準(α)と比較してp値を評価します。p値が有意水準以下であれば帰無仮説を棄却し、対立仮説を採択します。
仮説検定は、実験デザインやデータ分析の重要な部分であり、統計的推論の基本的な方法です。統計を学ぶ学生、若手研究者、データ分析に関心のあるビジネスパーソンにとって、これらの手順や概念を理解することは非常に重要です。
有意差検定との違い
有意差検定は、異なるグループ間で統計的に有意な差があるかを確認する仮説検定です。以下に、いくつかの主要な有意差検定の方法を紹介します。
t検定: 2つのグループ間の平均値の差を比較する検定です。片側検定と両側検定があり、サンプルサイズが小さい場合に使用されます。
ANOVA(分散分析): 3つ以上のグループ間の平均値の差を比較する検定です。複数のグループを同時に比較することで、より複雑なデータの分析が可能です。
χ2検定(カイ二乗検定): カテゴリカルデータのグループ間の頻度の差を検証する検定です。観察された頻度と期待される頻度の間に有意な差があるかを確認します。
これらの手法は、統計を学ぶ学生や若手研究者、データ分析に関心のあるビジネスパーソンにとって基本的なスキルです。有意差検定は仮説検定の一種で、特にグループ間の差異に焦点を当てています。特定の実験や調査でグループ差異が重要な場合に有効です。仮説検定と有意差検定を使いこなすことで、統計的なデータ分析においてより正確で信頼性の高い結論を導くことができます。
有意差検定の種類と手法
有意差検定は、データに基づいて仮説を検証するための重要な統計手法です。統計を学ぶ学生、若手研究者、データ分析に関心のあるビジネスパーソンにとって、この検定手法を適切に選び、正確に実施することは不可欠です。有意差検定には、t検定、カイ二乗検定、ANOVA(分散分析)が含まれます。t検定は2つのグループ間の平均値の差を比較するために使われ、カイ二乗検定はカテゴリカルデータの関係性を明らかにします。ANOVAは3つ以上のグループ間で平均値の差を評価します。各検定手法にはサンプルサイズやデータ分布の正規性といった注意点があるため、それぞれの方法を理解し、適切に選ぶことが成功への鍵となります。
平均値の比較
平均値の比較は、2つ以上のグループ間で平均値が異なるかどうかを検証する際に用いる重要な手法です。最も一般的な手法には、t検定とANOVAがあります。
t検定は、2つのグループの平均値を比較する方法です。母集団の標準偏差がわかっている場合は標準t検定を使用し、標準偏差が不明な場合はWelchのt検定を用います。t検定を実施する際には、対象データが正規分布に従っていることが前提となります。
ANOVAは、3つ以上のグループ間の平均値を比較する際に使います。ANOVAの基本的な考え方は、各グループ間の変動とグループ内の変動を比較し、全体として有意差があるかを判断することです。統計的に有意な差が認められた場合は、事後分析(例: TukeyのHSDテスト)を行い、どのペアが有意に差があるかを特定します。
これらの手法を用いることで、データの背後にある統計的有意差をより深く理解し、効果的なデータ分析が可能となります。
カイ二乗検定とは?
カイ二乗検定とは、カテゴリカルデータの分析で使用される統計手法です。この手法は、観察された頻度と期待された頻度が一致しているかどうかを確認するために有用です。
独立性のカイ二乗検定は、2つのカテゴリカル変数が独立しているかどうかを判断するために使用されます。例えば、性別と購入行動の間に関係があるかを検証する際に利用されます。この検定により、変数間の関連性を客観的に評価できます。
適合度のカイ二乗検定は、観察データが理論的な分布と一致しているかを確認するために使用されます。例えば、サイコロの出る目が均等に分布しているかどうかを検証する際に適用されます。この手法により、データが仮定する分布にどれだけ適合しているかを評価可能です。
これらの検定手法を理解し正しく実施することで、データの分析能力を向上させることができます。

その他の有意差検定手法
有意差検定には、平均値の比較やカイ二乗検定以外にも多くの手法があります。ここではいくつかの代表的な技法を紹介します。まず、マン・ホイットニーのU検定は2つの独立したサンプルの中央値を比較する手法です。この方法は、データが正規分布しない場合にt検定の代替手法として使用されます。次に、ウィルコクソンの符号付順位検定は対応のある2つのサンプル間の差を比較する方法で、同一対象に対する異なる条件の測定結果を比較する場合に用いられます。また、クラスカル・ウォリス検定はANOVAのノンパラメトリック版とされ、3つ以上の独立したサンプルの中央値の差を比較する手法です。この検定もデータが正規分布していない場合に使用されます。これらの手法を理解し適切に選ぶことで、統計的有意差の分析がより確実になり、研究やデータ分析の精度が向上します。
有意差検定を実施する際の重要ポイント
統計的有意差検定は、データ分析や研究に欠かせない手法です。まず、検定を行う前にサンプル数が十分であることを確認してください。サンプルサイズが不十分だと、検定結果が信頼できなくなる可能性があります。また、データの正規性や分散の等質性も考慮する必要があります。不適切な検定手法を選ぶと、結果が誤解されるリスクがあります。検定手法を選ぶ際には、データの特性に最も適した方法を選択し、解釈する際の注意点についても十分に理解しておくことが重要です。これらの基本概念を理解することで、より信頼性の高いデータ分析を行うことができます。
サンプル数の影響
有意差検定において、サンプル数は結果に大きな影響を与えます。サンプル数が多いほど、統計的検定の結果の信頼性が高まるため、十分なサンプル数を確保することが重要です。例えば、小さなサンプルサイズの場合、真の差異が存在していても検出できないことがあります。一方で、非常に大きなサンプルサイズでは微小な差異でも有意とされ、実際の意味が曖昧になることがあります。そのため、サンプルサイズの適切な設定が必要です。事前に必要なサンプルサイズを計算するためのツールや方法が提供されていますので、それを利用して適切なサイズを判断しましょう。また、効果量を考慮して検出力分析を行うことで、より精度の高いサンプルサイズの設定が可能です。
データの特性を理解する
有意差検定を行う前に、検定対象のデータの特性を理解することが重要です。例えば、データが正規分布に従うか、変数間の関係性、外れ値の有無などを確認する必要があります。データの特性を理解せずに検定を行うと、結果が誤った解釈につながる危険性があります。
例えば、データが正規分布に従わない場合は、非パラメトリック検定を検討しましょう。また、外れ値が存在する場合は、その影響を考慮するためにロバストな手法を用いることが有効です。データの分布や特性に応じた適切な検定手法を選択することで、より正確な結果を得ることができます。
統計を学ぶ学生や若手の研究者、データ分析に関心のあるビジネスパーソンにとって、これらの基本概念や手法を理解することは、質の高いデータ解析のための初歩的で重要なステップです。データの特性を把握し、有意差検定を適切に実施することで、信頼性の高い結果を得て、その結果を基にした意思決定も向上します。
有意差検定を簡単に理解するためのポイント
有意差検定は統計学の重要な手法で、データ間の差が偶然である可能性を評価します。統計を学ぶ学生、若手研究者、データ分析に関心のあるビジネスパーソンがこの手法を正しく理解し活用することは非常に必要です。まず、有意差検定の基本概念を把握しましょう。具体的には、帰無仮説と対立仮説を設定し、p値を計算することで観察された差が偶然かどうかを判断します。また、検定手法としてはt検定、カイ二乗検定、ANOVAなどがあります。注意点として、サンプルサイズと効果サイズの重要性、検定の前提条件の確認が挙げられます。これらを理解することで、統計的な検証がより信頼性の高いものとなります。
有意差検定を簡単にする方法
有意差検定を簡潔に理解するためには、以下のステップを踏むことが有効です。
まず、仮説設定を行います。帰無仮説(差がない)と対立仮説(差がある)を明確に設定することが重要です。これにより、検定の目的が明確になります。
次に、検定を実施するために必要なデータを収集します。データは信頼性が高く、バイアスのないものを選ぶことが必要です。バイアスがあると結果の信憑性が低下します。
適切な検定手法の選択も重要です。t検定、カイ二乗検定、ANOVAなど、多岐にわたる手法から比較対象やデータの種類に応じて最適なものを選びましょう。それぞれの手法には特性があるため、選択を誤ると正確な解析が難しくなります。
最後に、有意水準の設定を行います。通常は5%(p < 0.05)を設定しますが、研究の目的や分野によって適宜調整が必要です。この設定により、結果の解釈が統一されます。
これらのステップを踏むことで、統計的有意差の基本概念や検定手法を理解し、実際のデータ分析に効果的に活用することができます。
実際にデータを使用した比較と分析
具体的なデータを使用して有意差検定を実施するプロセスを紹介します。ここでは、一例としてt検定を用いた比較と分析の手順を説明します。
まず、例題を設定します。例えば、ある学校の二つのクラス(クラスAとクラスB)の数学テストの点数に差があるかどうかを調べます。各クラスの数学テストの点数を収集します。以下のデータがあるとします。
クラスA: 85, 90, 76, 92, 88, 74
クラスB: 78, 82, 74, 86, 80, 77
次に、仮説を設定します。帰無仮説は「クラスAとクラスBの数学テストの点数に有意な差はない(平均値は等しい)」であり、対立仮説は「クラスAとクラスBの数学テストの点数には有意な差がある(平均値が異なる)」です。
次に、t検定を実施します。エクセルの機能を使用して検定を実施すると、p値が得られます。仮にp値が0.03であったとします。
最後に、結果を解釈します。設定した有意水準(通常0.05)と比較して、p値=0.03は0.05よりも小さいため、帰無仮説を棄却し、クラスAとクラスBの数学テストの点数に有意な差があると結論づけます。
このように、具体的な手順に従って有意差検定を行うことで、データに基づいた客観的な結論を得ることができます。
有意差が「ない」となる場合の解決策
統計的有意差が得られない場合、それは結果の解釈とその後の対応において重要なポイントです。まず、有意差がない結果が示す可能性の一つは、サンプルサイズが不足していることです。十分なサンプルを確保することでデータの信頼性が向上します。また、検定手法や仮定の適合性を再評価することも必要です。例えば、選択した統計手法がデータ特性に適していない場合、結果が有意差を示さないかもしれません。最後に、統計的有意差が得られないこと自体が重要な発見である場合もあります。これは、実際に効果が存在しないという結論を支持する根拠となるからです。これらのポイントを踏まえ、統計解析を実施する際には常に批判的にデータと向き合う姿勢が求められます。
なぜ有意差が「ない」とされるのか
統計的有意差がないとされる理由は、主に以下の要因です:
サンプルサイズが小さい場合、統計的検出力が不足し、有意差を見つける能力が低下します。これにより、真の効果があっても検出できないことが多くなります。また、効果量が小さい場合、サンプルデータから有意差を見つけることが困難です。これも真の効果が存在しても、効果が微小であるため検出されにくくなります。
さらに、データのばらつきが大きい場合、ばらつきが真の効果を隠してしまい、有意差が現れにくくなります。ばらつきが大きいと、結果がノイズに埋もれてしまい、統計的な有意性が見えにくくなります。
最後に、不適切な検定方法を選択すると、有意差を適切に検出できません。データや研究目的に適した統計検定を選ぶことが重要です。適切な検定方法を使用することで、統計的有意差を正確に判断できます。
これらのポイントを理解し、統計的有意差を正しく解釈することで、より精緻なデータ分析が行えるようになります。
有意差がない場合の対策
有意差がない結果を得た場合、それをどのように解釈し次のステップをどう計画するかが重要です。以下にいくつかの対応策を示します:
サンプルサイズを増やす:サンプルが小さすぎると有意差が得られないことがあります。サンプルを増やすことで統計的検出力を高め、より信頼性の高い結果を導くことができます。
効果量を確認する:効果量(Cohenのdなど)を計算し、どれほどの効果があるかを明確にします。効果量が小さい場合でも、実務的や理論的に意味があるかを考察することが重要です。
ばらつきを減らす:データのばらつきを減少させるため、データ収集方法や条件を見直します。たとえば、実験条件の均一性を高めることで得られるデータの一貫性が増します。
適切な統計検定を選ぶ:使用した統計検定が適切であったか再確認し、異なる統計手法を試みることで有意差を見出せる可能性があります。使用する検定方法の選択は慎重に行いましょう。
結果の再現性を確認する:複数のデータセットや異なる条件下で同じ結論が得られるか確認します。再現性が高い結果は信頼性が向上します。
理論の見直し:得られた結果が既存の理論や仮説とどのように関連するか再考します。結果に基づき、仮説の変更や新たな理論の提案が必要となる場合もあります。
これらの対策を講じることで、有意差がない結果をより深く理解し、次の研究やデータ分析に役立てることができます。


